Предсказываем переменное будущее
→ о простом линейном регрессионном анализе
→ о диаграммах разброса и видах зависимостей
→ о диаграммах разброса и видах зависимостей

день 06
Сегодня на волнах нашего дата-эфира
Начинаем вторую половину Марафона с понимания простого линейного регрессионного анализа — что это такое, зачем нужно и как использовать на практике. Тема не сложная, но очень интересная
Зачем нужен регрессионный анализ
Мы касаемся темы регрессионного анализа, поскольку эта функциональность присутствует во многих инструментах анализа и визуализации данных.
Регрессионный анализ — набор статистических процедур для изучения зависимости между случайными переменными. Он включает в себя множество методов моделирования и анализа взаимосвязей между зависимой переменной и одной или несколькими независимыми переменными.
Регрессионный анализ помогает понять, как «типичное» значение одной зависимой переменной (которую мы и хотим спрогнозировать) изменяется при изменении одной из независимых переменных.
Регрессионный анализ используется для прогнозирования и классификации — во многом, эти же задачи решаются инструментами машинного обучения. Мы же рассмотрим сегодня один из методов регрессионного анализа — простую линейную регрессию.
Регрессионный анализ используется для прогнозирования и классификации — во многом, эти же задачи решаются инструментами машинного обучения. Мы же рассмотрим сегодня один из методов регрессионного анализа — простую линейную регрессию.
О линейной регрессии
Для того, чтобы лучше понять простой линейный регрессионный анализ, немного вспомним школьную алгебру.
Вспомните простые линейные уравнения вида y = ax + b. Они однозначно описывают взаимосвязь между двумя переменными x и y. Например, если мы скажем, что y = 3x + 5, то если x = 0, то y = 5. В этом случае коэффициент корреляции всегда будет равен 1 — идеальная связь, где мы всегда можем предсказать значение y по значению x.
Вспомните простые линейные уравнения вида y = ax + b. Они однозначно описывают взаимосвязь между двумя переменными x и y. Например, если мы скажем, что y = 3x + 5, то если x = 0, то y = 5. В этом случае коэффициент корреляции всегда будет равен 1 — идеальная связь, где мы всегда можем предсказать значение y по значению x.

При анализе данных, собранных из реальной жизни, построить (вывести) такие же уравнения с единичным коэффициентом корреляции сложно. Просто потому, что жизнь гораздо сложнее — даже самые сильные наблюдаемые явления в реальной жизни редко являются идеальными с точки зрения математики, другими словами не линейно зависимыми. То есть, мы почти никогда не можем со абсолютно полной уверенностью предсказать значение чего бы то ни было, не можем вывести закон или формулу со 100%-ной точностью.
Но мы можем попытаться сделать максимальное точное приближение.
Посмотрим на взаимосвязь между количеством лет образования (т.е. его уровнем) и заработком. В целом, мы понимаем, что более образованные люди получают больше. Но эта связь не идеальна: Билл Гейтс не закончил колледж, а многие ученые и профессора получают довольно низкую зарплату. Поэтому, на практике мы не стремимся получить идеальные линейные взаимосвязи, но стремимся найти полезные для наших задач.
Но мы можем попытаться сделать максимальное точное приближение.
Посмотрим на взаимосвязь между количеством лет образования (т.е. его уровнем) и заработком. В целом, мы понимаем, что более образованные люди получают больше. Но эта связь не идеальна: Билл Гейтс не закончил колледж, а многие ученые и профессора получают довольно низкую зарплату. Поэтому, на практике мы не стремимся получить идеальные линейные взаимосвязи, но стремимся найти полезные для наших задач.

Мы хотим уметь предсказывать некоторый фактор чуть более точно. Линейный регрессионный анализ позволяет нам строить прогнозы для переменной на основе значений другой переменной. У нас есть приближенный закон ее изменения
Например, зная количество лет образования человека, мы смогли бы предсказать диапазон его заработка чуть более точно, чем не зная его образования (и не имея «предсказательного закона»).
График и формула простой линейной регрессии
Мы уже знаем, что взаимосвязь двух переменных можно изучать с помощью диаграмм рассеяния и коэффициента корреляции. Эти два метода можно отнести к методам простого линейного регрессионного анализа.
напоминание про коэффициент корреляции
Напомним, что коэффициент корреляции выражает силу взаимосвязи между двумя переменными. Коэффициент может принимать значения от -1 до 1. Чем его значение ближе к 0, чем связь слабее. Чем значение ближе к границам интервала (к -1 или к +1) — тем сильнее.
Так вот. Если посмотреть на математическое определение линейной регрессии, то ее можно описать как «метод аппроксимации зависимостей между входными и выходными переменными на основе линейной модели». Если перефразировать это определение, то можно сказать, что простая линейная регрессия пытается создать некоторое уравнение, которое опишет имеющиеся у нас данные максимально точно — какие значения они принимают сейчас и какие, скорее всего, еще могут принять.

Например, у нас есть данные по распределению некоторого показателя (кстати, что это могло бы быть?). Создание регрессионной модели здесь сводится к построению линии регрессии (она отмечена синим) на основе уравнения регрессии.

из чего состоит уравнение регрессии?
- y — зависимая переменная, а x — независимая переменная
- a- коэффициент наклона (то, насколько линия визуально наклонена)
- b — константа, которая отвечает за смещение линии по оси Y
Основной задачей является определение параметров b и a. Они определяются таким образом, чтобы сумма квадратов отклонений точек, соответствующих реальным наблюдениям данных, от линии регрессии была бы минимальной. Обычно используется метод наименьших квадратов.
То есть, если вы видите уравнение y = 91x — 74 и знаете, что оно описывает взаимосвязь между, например, ростом человека и его весом, то можно сделать предсказание: человек с ростом 1,8 метра будет иметь массу тела 89,8 кг, потому что y = 91(1,8) — 74 = 89,8. Разумеется, это довольная простая модель. На практике чаще используются более сложные модели, с несколькими переменными и дополнительными параметрами. Но наш пример дает общее понимание и базу для изучения регрессионного анализа.
→ подробнее про линию регрессии
→ подробнее про линию регрессии
Для оценки «качества модели» используется коэффициент детерминации, показывающий, насколько расчетные параметры модели, то есть сама модель, объясняют зависимость и изменения изучаемого параметра — Y от исследуемых факторов — X. Коэффициент детерминации может быть в диапазоне от 0 до 1. Чем больше коэффициент, тем лучше. Считается, что если коэффициент детерминации выше 0,8, то модель хорошо описывает данные, а если меньше 0,5, то смысл такой модели сомнителен.
Вы можете провести вертикальные линии от каждой из точек к линии регрессии. Длина каждой такой линии будет ошибкой предсказания (отклонения) для каждой точки. Разница между каждой точкой и линией регрессии отражает изменчивость в данных, которая не объясняется уравнением прямой.
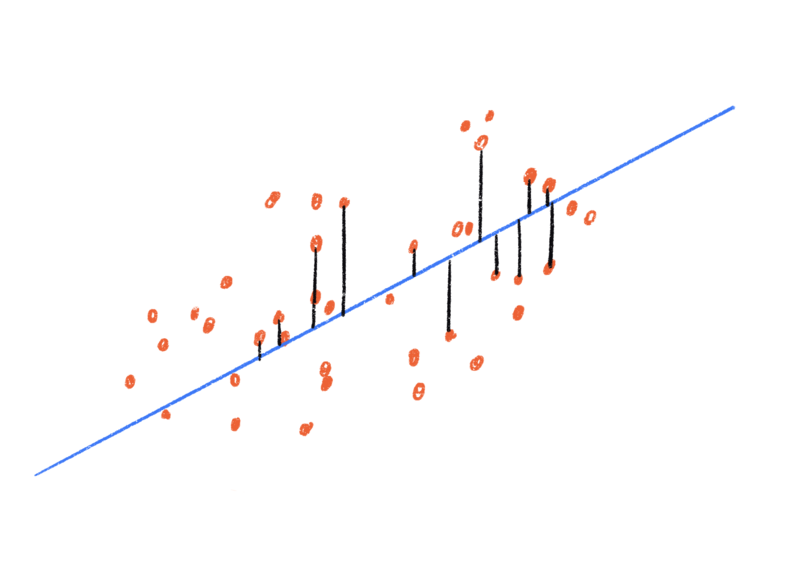
Диаграмма разброса
Как вы могли заметить, модель линейной регрессии отмечается на диаграмме разброса или диаграмме рассеяния. Диаграмма показывает распределение элементов множества в плоскости между двумя переменными. Значения одного независимого параметра откладываются по оси X, значения второго зависимого параметра — по оси Y.

Существует большое количество паттернов корреляционной связи — положительная или отрицательная, сильная или слабая, линейная или нелинейная. В определении типа корреляции будет помогать коэффициент корреляции и визуальное представление данных на диаграмме рассеяния.
Управление ассортиментом в Утконос ОНЛАЙН

Данила Наумов
Директор по данным, Утконос ОНЛАЙН
Когда появилась задача расширить ассортимент онлайн-ритейлера, возник вопрос:
какие категории следует расширять в первую очередь? Как расширение ассортимента в разных категориях влияет на изменение выручки?
Что решили сделать?
Для решения проблемы приоритезации команда Утконос воспользовалась
регрессионным анализом. Построили регрессионную зависимость выручки и
пенетрации в чеке от количества товаров в категории. Пенетрация — доля чеков (заказов), в которой есть хотя бы один товар из категории.
Для каждой продуктовой категории (включая подкатегории разного уровня) были построены диаграммы рассеивания по медианным значениям:
→ выручки в зависимости от количества товаров на складе
→ очищенной выручки в зависимости от количества товаров на складе
→ % пенетрации в зависимости от количества товаров на складе

Аналитики искали категории, которые могут сильнее «выстрелить».
Зеленой пунктирной чертой на графиках отмечено текущее количество товаров на складе в категории.
На всех трех графиках точками отмечены фактические медианные значения, а красная линия описывает эти точки.
По ней можно предположить, насколько насыщена рассматриваемая категория. Чем линия более горизонтальна, тем категория более насыщена. Значит, при увеличении ассортимента значительных изменений в выручке или пенетрации не ожидается.
Зеленой пунктирной чертой на графиках отмечено текущее количество товаров на складе в категории.
На всех трех графиках точками отмечены фактические медианные значения, а красная линия описывает эти точки.
По ней можно предположить, насколько насыщена рассматриваемая категория. Чем линия более горизонтальна, тем категория более насыщена. Значит, при увеличении ассортимента значительных изменений в выручке или пенетрации не ожидается.
Что получилось?
Сложно привести все результаты кейса, но разница в эффективности добавления в ассортимент разных категорий хорошо показывается линиями регрессии. Так, например, категория Молока перенасыщена, а кисломолочных продуктов может дать положительный эффект.


Так как сравнивать десятки графиков по категориям трудоемко, то аналитики также разработали модель расчета, основываясь на коэффициентах регрессий. Таким образом, специалисты, которым нужно добавить 100 новых позиций, вводят целевую цифру и получают распределение по продуктовым категориям. Сколько из 100 позиций должно быть отдано, например, десертам, а сколько — кисломолочным продуктам, причем так, чтобы максимизировать потенциальную выручку и пенетрацию в чеке.
а теперь... Практика

Для практики дня 06 мы предлагаем вам изучить доклад, подготовленный программой развития ООН, точнее даже не доклад — а его краткое изложение на русском языке (конечно, если вы владеете английским, то можете посмотреть и полную версию).
Доклад о человеческом развитии 2020
Резюме на русском языке. Юбилейный 30-й Доклад о человеческом развитии 2020 является новейшим из серии глобальных Докладов о человеческом развитии, которые публикуются Программой развития Организации Объединенных Наций (ПРООН) с 1990 года в качестве независимого, аналитически и эмпирически обоснованного обсуждения важнейших вопросов, тенденций и политических мер в области развития.
Задание 01.
Нам интересно посмотреть на закономерности, которые были выявлены исследователями. Некоторые из них представлены в кратком изложении выводов по человеческому развитию, которое можно скачать выше.
→ 01.1. Найдите интересные для себя закономерности и корреляции. Могли бы вы предположить нечто такое, не имея обоснованных выводов на основе данных? Как может поменяться ваше мнение теперь, когда вы знаете о такой информации?
→ 01.2. Если чувствуете себя более уверенно с данными, попробуйте скачать несколько наборов данных с сайта прямо здесь. Данные хранятся в нескольких категориях, в которых можно найти корреляционную зависимость. Можно изучить, например, подростковую рождаемость (раздел Gender) и общий уровень образования у женщин (раздел Education).
→ 01.3. Попробуйте посчитать корреляцию и построить линию регрессии на основе скачанных данных.
→ 01.1. Найдите интересные для себя закономерности и корреляции. Могли бы вы предположить нечто такое, не имея обоснованных выводов на основе данных? Как может поменяться ваше мнение теперь, когда вы знаете о такой информации?
→ 01.2. Если чувствуете себя более уверенно с данными, попробуйте скачать несколько наборов данных с сайта прямо здесь. Данные хранятся в нескольких категориях, в которых можно найти корреляционную зависимость. Можно изучить, например, подростковую рождаемость (раздел Gender) и общий уровень образования у женщин (раздел Education).
→ 01.3. Попробуйте посчитать корреляцию и построить линию регрессии на основе скачанных данных.
а теперь... Материалы

Объяснение темы и сопровождение кейсами из бизнеса и жизни
Статистический базис знаний для понимания темы
Спасибо за эфир!
Отлично разобрались с назначением и смысловым наполнением линейной регрессии. Спасибо, что читаете лонгрид до конца! Завтра посмотрим на постановку гипотез и проведение экспериментов.
